By Jaan Kalda (TalTech).
In the figure below, the ellipse is a real image of a circle created by an ideal thin lens. The point F is the closer-to-the-ellipse main focus of the lens. Optical axis lies in the plane of this figure. Construct geometrically the centre O of this thin lens. Use the figure in .ggb format.
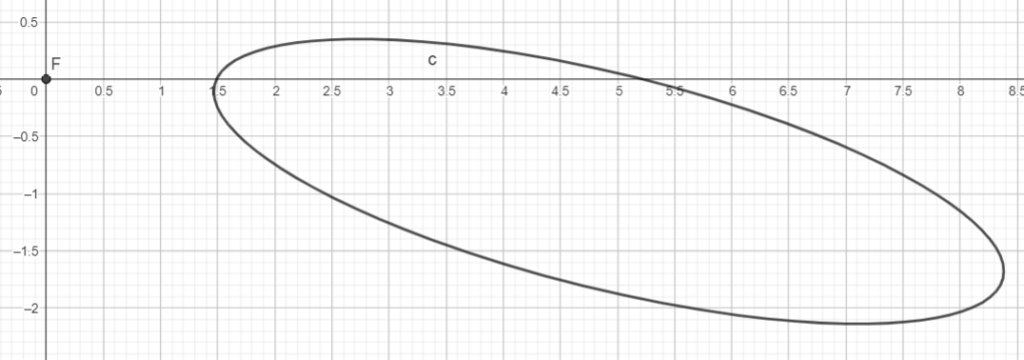
For an answer-only solution, please submit the coordinates of the point O with five decimal digits (if this is impossible due to technical reasons, send a sketch – a photo/scan – of your geometrical construction). With your full solution, please submit also a Geogebra file (.ggb), and if you did not send it earlier due to technical reasons, state in your e-mail the coordinates of the point O with five decimal digits.
Remark 1: You are not supposed to use trial-and-error approach (e.g. looking for such a position of some point by which three points are collinear or two points coincide etc). The centre of the lens should come out as an intersection point of some lines or curves without any room for trials.
Remark 2: Please download and use the Geogebra file with the ellipse and the focus. With the Geogebra (online app: https://www.geogebra.org/classic), you may use the functionality available through the menu buttons (except the Locus, Polar, Complex numbers, Best Fit Line, functions tools, and tools with numeric input). You are not allowed to make numerical calculations in Geogebra and enter calculated point coordinates. The available tools are shown below.

Please submit the solution to this problem via e-mail to physcs.cup@gmail.com. First hints will appear here on 17th December 2023. After the publication of the first hint, the base score is reduced to 0.9 pts. For full regulations, see the “Participate” tab. The first intermediate results for the Problem 2 will be drawn after 13:00 GMT, 10th December 2023.
