Contributed by Lev Melnikovsky ( Kapitza Institute for Physical Problems ).
The equilibrium shape of bodies in zero-gravity is determined by the minimum of their surface energy. At low temperature, the equilibrium shape of crystals may have flat facets. The parts of the crystal surface that have a small angle \phi with the facet are in fact staircases of rare steps on this facet, see the figure below. The height of such steps is equal to the period of the crystal lattice h .
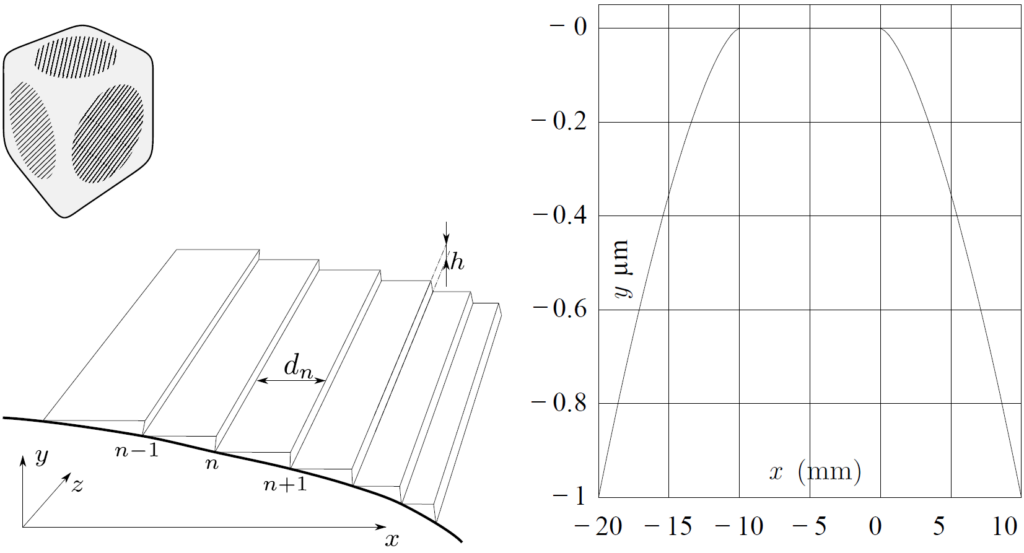
Equilibrium surface profile y(x) of a certain crystal and the corresponding microscopic staircase are shown schematically in the figure on left, where n denotes the step number, counting from x=0 .
The profile shape of this crystal is shown in the figure on right; at x >0 it can be approximated as y(x) = -(x/\lambda)^{3/2} h , \lambda = 45μm, h= 0.3nm .
This crystal has been studied by the third problem of the second European Physics Olympiad: it has been shown that the distance d_n between two adjacent steps for n \gg 1 is given by d_n= 30μm n^{-1/3},
and that the interaction energy E of two steps depends on the distance d between them as E(d) = \mu \, d^{-2} . Here it is assumed that only adjacent steps interact, and the energy E(d) is given per unit length of of the steps (i.e. per the length in the z -direction in the figure).
Assuming that in addition to the interaction energy, the existence of each step contributes the energy per unit length of the step \beta= 4 \cdot 10^{-15} J/m, find the value of the constant \mu in this expression using the data and graphs given above.
Chinese translation of the Problem No 2.
Please submit the solution of this problem via e-mail to physcs.cup@gmail.com. First hints will appear here on 22nd December 2019, but after the publication of the first hint, the base score is reduced to 0.9 pts. For full regulations, see the “Participate” tab.
