By Jaan Kalda (TalTech).
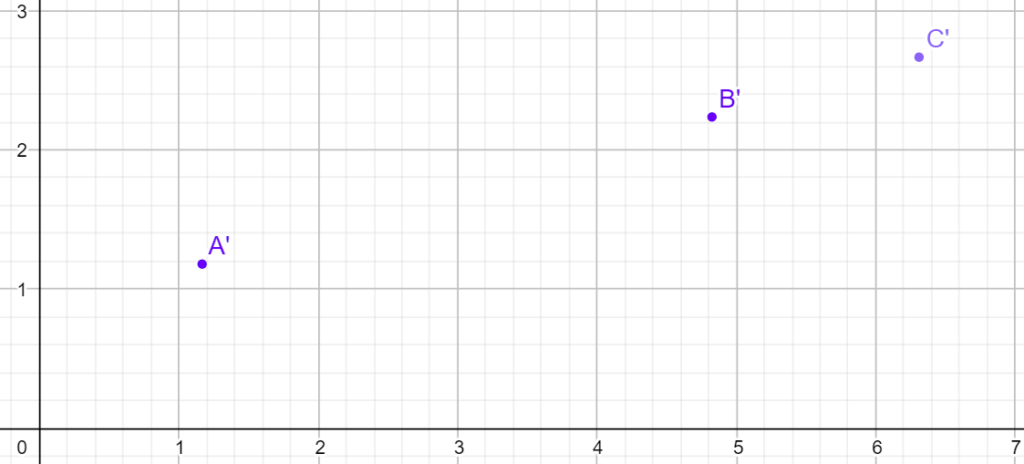
Four points, A, B, C and D lie on a straight line on equal distances from each other, i.e. |AB|=|BC|=|CD|. Figure below shows points A', B', and C' which are the images of the points A, B, and C created by a thin lens. The focal length, position and orientation of the thin lens are not known; the only thing what is known is that the optical axis of the lens lies in the plane of the figure. Construct geometrically the point D', the image of the point D. With your full solution, please submit also a Geogebra file (.ggb), and the coordinates of the point D' with three decimal digits.
Remark: Please download and use the Geogebra file with the images of the three points. With the Geogebra (online app: https://www.geogebra.org/classic), you may use the functionality corresponding to what can be done with a ruler and compass (drawing lines, perpendicular lines, finding midpoints, etc). You are not allowed to make numerical calculations in Geogebra and enter calculated point coordinates.
Please submit the solution to this problem via e-mail to physcs.cup@gmail.com. First hints will appear here on 6th November 2022. After the publication of the first hint, the base score is reduced to 0.9 pts. For full regulations, see the “Participate” tab. The intermediate results for the Problem 5 will be drawn after 13:00 GMT, 27th February 2022.
