By Jaan Kalda (TalTech).
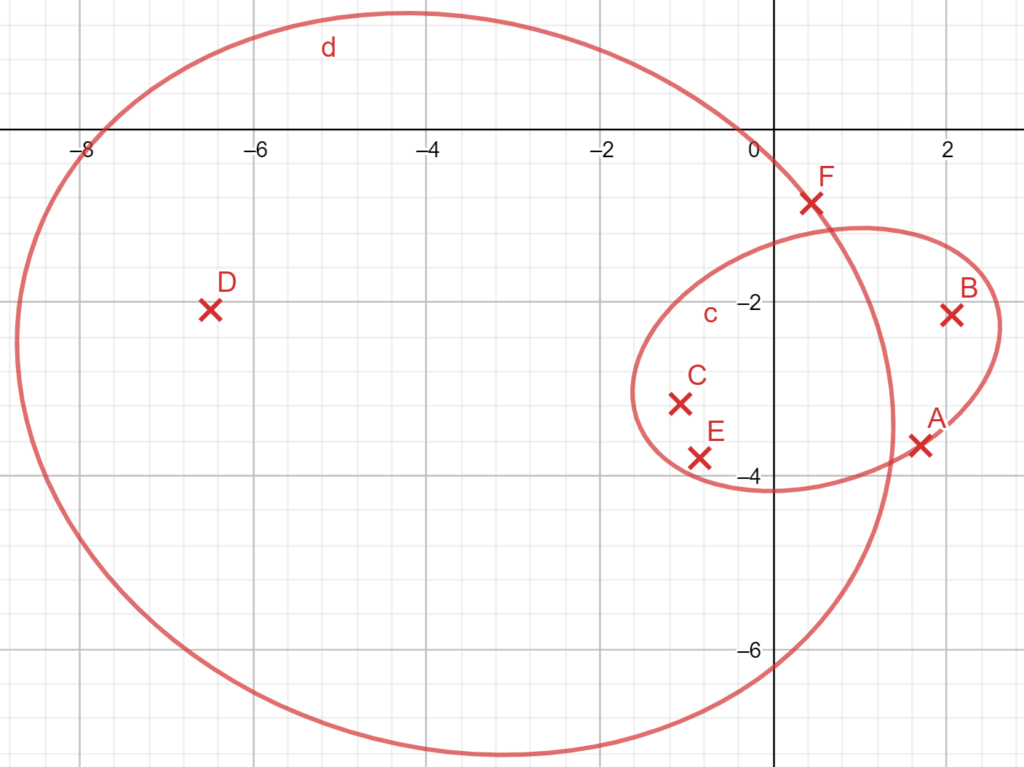
The two ellipses depicted in the figure below, available as a Geogebra file, represent real images of circles, created by an ideal thin lens. Both the ellipses and the main optical axis of the lens lay in the plane of the figure. Reconstruct the position of the lens (i.e. the position of the centre and the orientation). Remark: it is recommended to use Geogebra, https://www.geogebra.org/, either as an online service, or as a downloaded application. In you construction steps, you may use everything what Geogebra has to offer: drawing a line through two given points, drawing parallel and perpendicular lines to a given line through a given point, drawing tangents through a given point to a given shape (i.e. a given curve), finding intersection points of shapes (i.e. of curves or lines) , drawing circles with a given centre through a given point, or through three given points, or through two diametrically opposite points on it, drawing ellipse with given foci through a point laying on it, or through five given points. Trial-and-error approach (for instance, displacing a certain shape until three certain intersection points lay on a straight line) is not accepted. You are welcome to send me the .ggb files together with the solution. Alternatively, you may print the ellipses onto a sheet of paper and make constructions by hand using a ruler and a compass (be aware that there may be no solution if you start with arbitrarily positioned two ellipses of arbitrary shape, so make sure to either print the drawing, or take the initial shapes close enough to the provided one).
Chinese version of the Problem 5
Please submit the solution of this problem via e-mail to physcs.cup@gmail.com. For full regulations, see the “Participate” tab.
