by Jaan Kalda (TalTech).
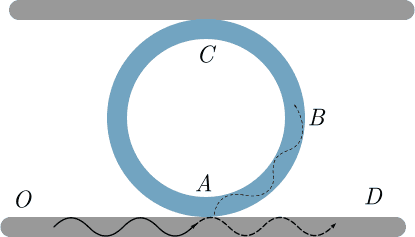
A circular resonator in fibre optics is made from one circular single-mode fibre coupled to two straight single-mode fibres as shown in the figure. In single-mode fibres, light propagation is essentially one-dimensional: the phase of the electric and magnetic fields in each cross-section of the fibre is constant. The couplings A and C between the circular fibre and the straight fibres are such that a very small fraction \alpha\ll 1 of light energy propagating in one of the fibres is transmitted through the coupling into the other fibre. Assume that the both couplings are identical. As a wave of amplitude E propagates in the circular fibre, a double-frequency light wave of amplitude \mathcal E is generated due to nonlinearity of the fibre (however, the double-frequency wave propagates linearly without generating a quadruple-frequency wave). We assume that the dispersion is negligible, i.e. the coefficient of refraction is the same for both the main wave, and for the double-frequency wave so that the increase \Delta \mathcal E in the amplitude of the double-frequency wave is proportional to the travel distance. Here we quantify the nonlinearity of the circular fibre with the constant \delta, such that if a wave of amplitude E travels through a semicircle ABC, the amplitude \mathcal E of the co-propagating double-frequency wave is increased by \Delta \mathcal E=\delta E^2; this expression is valid assuming that \delta \mathcal E\ll 1 (you can use this assumption). The coupling constant \alpha is a function of the frequency of the wave; here we denote the coupling constant for the main wave by \alpha, and assume that the coupling constant for the double-frequency wave equals to \alpha^2. The length of the circular fibre equals to an integer multiple of the wavelength of the main-frequency wave.
Laser light of intensity I_0=E_0^2 (with E_0 denoting the amplitude of the wave) and of a very long coherence length is directed into the bottom fibre at the input O; at the output D, both the main-frequency and double-frequency light will appear. For fixed values of I_0 and \delta, the intensity of the double-frequency light \mathcal I at the output depends on the coupling strength \alpha which can be easily controlled through the manufacturing process. Find the maximal value \mathcal I_m of \mathcal I, and the corresponding coupling strength \alpha_m (express in terms of I_0 and \delta; only closed-form expressions are accepted).
Hint 0, Hint 1, Hint 2, Hint 3, Hint 4, Best solutions and final results
Please submit the solution of this problem via e-mail to physcs.cup@gmail.com.
For full regulations, see the “Participate” tab.
