By Jaan Kalda
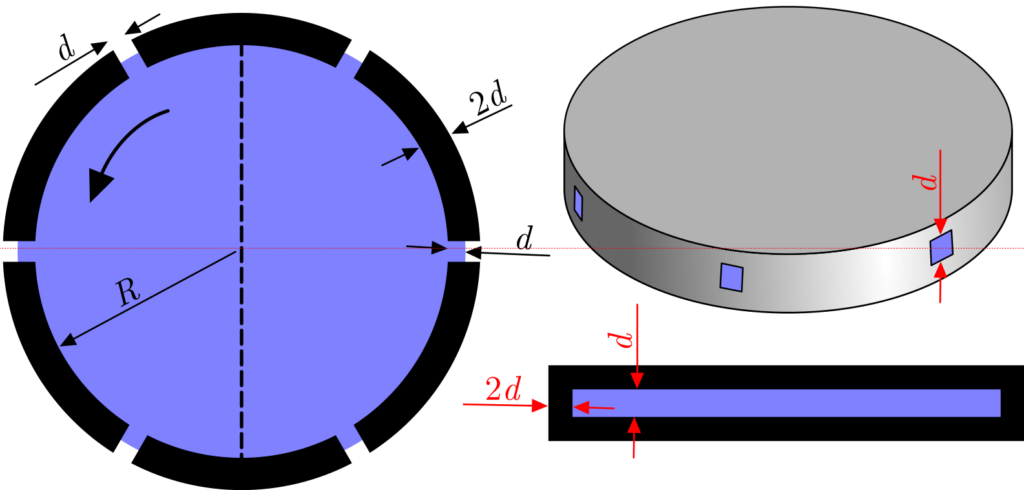
A thin cylindrical container of radius R, wall thickness 2d\ll R, and height h = d, filled with water, rotates at angular velocity \Omega. Six radial holes of h\times h square cross-section are made through the wall at 60° intervals (at clock positions 1, 3, 5, 7, 9, 11). Initially the holes are plugged so that water fills the region of radial distance r < R + d as shown in the figure. The surface tension \sigma \gg \rho d^2 R\Omega^2, where \rho denotes the water density, and the contact angle is 90°. Assume R \gg d and neglect gravity. Outside air pressure is atmospheric.
All plugs are removed simultaneously; immediately after removal, the water is still at rest in the co-rotating frame, but now water can flow through the holes. Let t = 0 be when water in one of the holes has displaced by x with x \ll d; it appears that by t = T_1, it has displaced by 2x.
A radial thin partition is now installed along the line connecting the clock positions of 12 and 6, creating two semicircular compartments with three holes in each. The experiment is repeated.
Find T_2^2-T_1^2, where T_2 is the time from displacement x to displacement 2x in the hole at 3 o’clock of the partitioned case.
Please submit the solution to this problem via e-mail to physcs.cup@gmail.com. After the publication of the first hint, the base score is reduced to 0.9 pts. For full regulations, see the “Participate” tab.
