By Jaan Kalda (TalTech).
Since the rotation speed is small, R\ll \sqrt{\rho/\mu\omega}, the charge carriers reach a quasi-equilibrium: the Lorentz force and Coulomb force cancel each other out (we’ll discuss this strong inequality later in more details):
\vec E=-\vec v\times\vec B=\vec r_\perp\omega B,where \vec r_\perp denotes the perpendicular-to-the-rotation-axis component of the radius vector \vec r. From here, using vector calculus and the Gauss law, it is easy to deduce that there will be a homogeneous charge density
\rho=\varepsilon_0\mathrm{div}\vec E=2\varepsilon_0\omega B,as \mathrm{div}\vec r_\perp=2. The same conclusion can be reached using the Gauss law in integral form, by applying it to a coaxial cylinder of height h and radius r that is fully inside the ball. It can be also easily deduced by using the Gauss law in integral form that the electric field caused by the homogeneous spherical volume charge of density \rho=2\varepsilon_0\omega B equals to \vec E_v=\frac 23\omega B\vec r. Hence, the contribution of the surface charge to the electric field inside the ball equals to
\vec E_s=\vec E- \vec E_v=\frac 13\omega B(2x\hat x -\vec r_\perp),\;\;\;\;\;\; (1)
where \hat x denotes a unit vector parallel to the x-axis. This expression of the electric field is linear in coordinates, meaning that the potential inside the ball is a quadratic polynomial of the coordinates. This is a property of the electric field inside a homogeneously charged ellipsoids: if the ellipsoid’s axes are oriented along the x, y and z axis then \varphi=ax^2+by^2+cz^2, where the constants a, b and c depend on the charge density and the shape of the ellipsoid. If we overlap spheroids of equal and opposite charge densities, the electric field inside the overlapping region takes form
\varphi=(a-a')x^2+(b-b')(y^2+z^2)\;\;\;\;\;\; (2).
Since there are no charges inside the overlapping region, the divergence of the electric field is zero (i.e. there is no electric field flux through any closed surface), hence (a-a')x^2+2(b-b')=0 and \varphi=A(2x^2-y^2-z^2). The constant A depends on the charge density of the spheroids, hence we can adjust the charge density to match the field given by Eq. (1). If we make the spheroids in shape very close to spheres, the residual (non-overlapping) charge becomes a surface charge, and Eq. (1) is satisfied within the entire sphere. Notice that for simplicity, we can take one of the spheroids to be exactly a sphere because in Eq. (2), we only need that a\ne a', b\ne b'.. Without limiting generality, we can assume that the spheroid fits into the sphere as shown in the figure, because a layer of arbitrary thickness can be shaved off without changing the field inside (where the field created by such a layer is zero). From this figure, we can see that
\sigma =\sigma_0\cos^2 \theta\;\;\;\;\;\; (3)
(if the spheroid is prolate and not oblate, it would be \sigma =\sigma_0\sin^2 \theta=\sigma_0(1-\cos^2)\;\;\;\;\;\; where the constant part can be dropped, because a spherical surface charge will create no field inside the sphere).
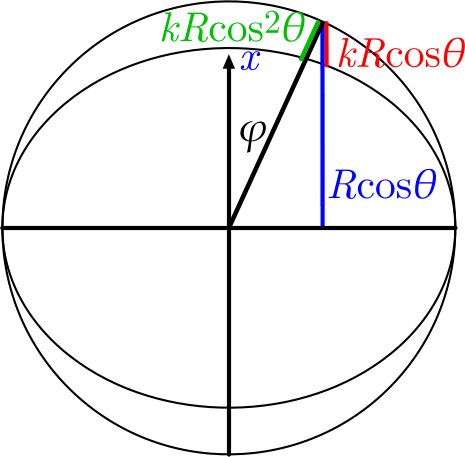
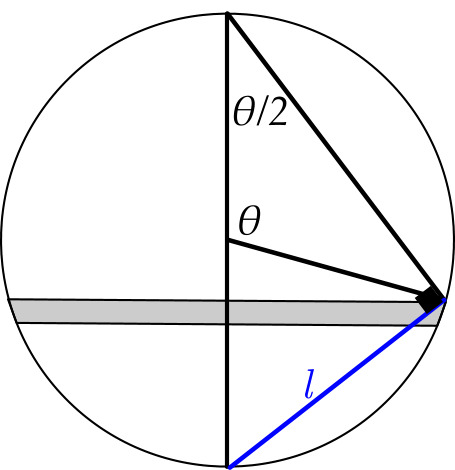
We know that the electric field inside the sphere has the required functional form Eq. (1), but we need to ensure that the field strength is correct. To that end, we require that Eqns. (1) and (3) create the same potential difference between the centre of the sphere, and its south pole. In the case of Eq. (1), expressing this potential difference is a trivial task yielding \varphi=\frac 13\omega BR^2. In the case of Eq. (3) we need to integrate: using the figure below,
\varphi =\frac 1{4\pi\varepsilon_0}\int_0^\pi\mathrm dq(\frac 1l-\frac 1R)=\frac 1{4\pi\varepsilon_0}\int_0^\pi\sigma_0\cos^2 \theta 2 \pi R^2\sin\theta\left[\frac 1{2R\sin(\theta/2)}-\frac 1R\right]\mathrm d\theta=\frac 2{15}\frac{\sigma_0R}{\varepsilon_0}.
Equating this to \frac 13\omega BR^2, we obtain \sigma_0=\frac 52 \varepsilon_0B\omega R.
Those who know about quadrupole field can now proceed with calculating the quadrupole moment of the sphere, but let us pretend we don’t know. We move the observation point from the south pole to distance L from the centre of the ball, and calculate using the cosine theorem and keep the second order terms of R/L.in Taylor expansion (the constant and linear terms cancel out during integration) . However, we need to keep in mind that while the total charge of the surface charge given by Eq. (3) is non-zero, the total charge of the ball is zero. All the other charges as distributed with spherical symmetry, hence the field created by them at the observation point is the same what would be if these charges were to be concentrated at the centre of the ball. Keeping all this in mind we obtain:
\varphi =\frac 1{4\pi\varepsilon_0}\int_0^\pi\sigma(\theta)\left[\left(L^2+R^2+2LR\cos\theta\right) ^{-1/2}-1/L\right]\mathrm dA=\frac 1{4\pi\varepsilon_0L}\int_0^\pi \sigma_0\cos^2 \theta\cdot 2 \pi R^2\sin\theta\left(\frac RL\right)^2\left(\frac 32\cos^2\theta-\frac 12\right)\mathrm d\theta=\frac {\sigma_0R^4}{2\varepsilon_0L^3}\left(\frac 35-\frac 13\right)=\sigma_0R^4\frac 2{15\varepsilon_0L^3}=\frac {B\omega R^5}{3\varepsilon_0L^3}.Therefore, the electric field at the observation point
E=\frac{\mathrm d\varphi}{\mathrm dL}=\frac {B\omega R^5}{\varepsilon_0L^4}.Now it is already easy to find the dipole moment induced on the other sphere (this is easily derived by considering two slightly displaced spherical volume charges of opposite sign) : =4\pi\varepsilon_0R^3.. Now we can find the force exerted to the dipole by differentiating the potential energy of the dipole -Ep over the distance while assuming that the dipole moment remains constant:
F=p\frac{\mathrm dE}{\mathrm dL}=16\pi\varepsilon_0 B^2\omega^2\frac {R^{13}}{L^9}.Throughout the problem, we assumed that the magnetic field inside the rotating sphere is constant and homogeneous. However, if the ball rotates too fast, eddy currents will oppose magnetic flux changes through material contours inside the conductor. In the case of AC currents, this results in magnetic field (and thereby current) restricted into a skin depth of thickness \delta = \sqrt{\frac{2\rho}{\mu\omega}}. Note that with the factor \sqrt{2}, this skin depth provides depth at which the field decreases by e times in one-dimensional problem statement; in our context, it is unimportant. If this depth is much larger than the radius of the ball, it means that the eddy currents are too weak to cause a skin effect, i.e. we can assume the magnetic field to be homogeneous throughout the sphere. Now, R\ll \sqrt{\frac{\rho}{\mu\omega}} is equivalent to the condition provided in the problem statement.
Please submit the solution of this problem via e-mail to physcs.cup@gmail.com. After the publication of the first hint, the base score is reduced to 0.9 pts. For full regulations, see the “Participate” tab.
