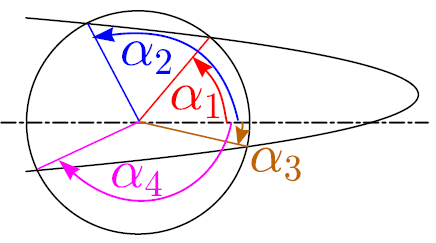
While all the correct solutions submitted during the first two weeks are careful algebraic/trigonometric calculations (in some cases fairly long), there exists a beautiful approach which is mathematically much simpler than the brute-force-solutions, but makes use of a not-too-well-known theorem about the intersection points of a parabola and a circle. More specifically, if a parabola and a circle intersect at four points the sum of polar angles \alpha_1, \alpha_2, \alpha_3 , and \alpha_4 (see the figure below) can take only certain discrete values. Note that there is another theorem regarding the sum of ordinates for these four points (assuming that the axis of the parabola is taken as the horizontal axis); that theorem can be used, too, to solve the given problem, although less conveniently than the theorem for the sum of angles. So, you can either use a brute-force- approach, or prove one of the two theorems mentioned above, and simplify thereby the further calculations drastically.
Few additional hints and comments. First, you need to consider positive values of v_0 only (downwards in the figure), and there are four possible values for v_0: one trivial, and three non-trivial ones.
Second, I was not very accurate while asking you to express answers algebraically as that would lead you to casus irreducibilis. Trigonometric expressions evaluated numerically are accepted.
