Theorem: if a parabola and a circle intersect at four points, the sum of polar angles \alpha_1+\alpha_2+\alpha_3+\alpha_4=2\pi n, where n is an integer (see the figure below). Proof: without restricting the generality of the foregoing, let the circle be of unit radius and centered at the origin, given by x^2+y^2=1. Let us consider the complex plane z=x+\mathrm i y ; then, the formula of the circle takes form z\bar z=1, where \bar z=x-\mathrm i y is the complex conjugate of z so that x=\frac 12 (z+\bar z) and y=\frac {\mathrm i}2 (\bar z-z). Then the formula of the parabola ax=b+cy-y^2 is rewritten as 2a(z+\bar z)=2b+2c\mathrm i(\bar z-z)+(\bar z-z)^2 . The intersection points satisfy both the equation of this parabola, and the equation of the circle from where we substitute \bar z=1/z; we end up in a fourth order algebraic equation for z, with the zeroth order term being equal to 1. This means that according to the Vieta’s formula, the product of the four roots z_1z_2z_3z_4=1. All these roots are on the unit circle and therefore z_i=\mathrm e^{\mathrm i\alpha_i}; consequently, \mathrm e^{\mathrm i(\alpha_1+\alpha_ 2+\alpha_ 3+\alpha_ 4)}=1 which proves the theorem.
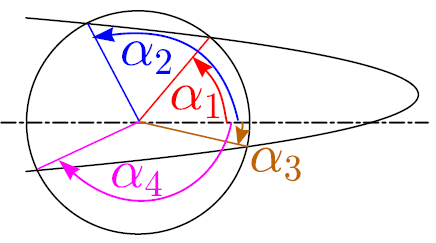
Using this theorem, there is no need for long mathematical calculations!
