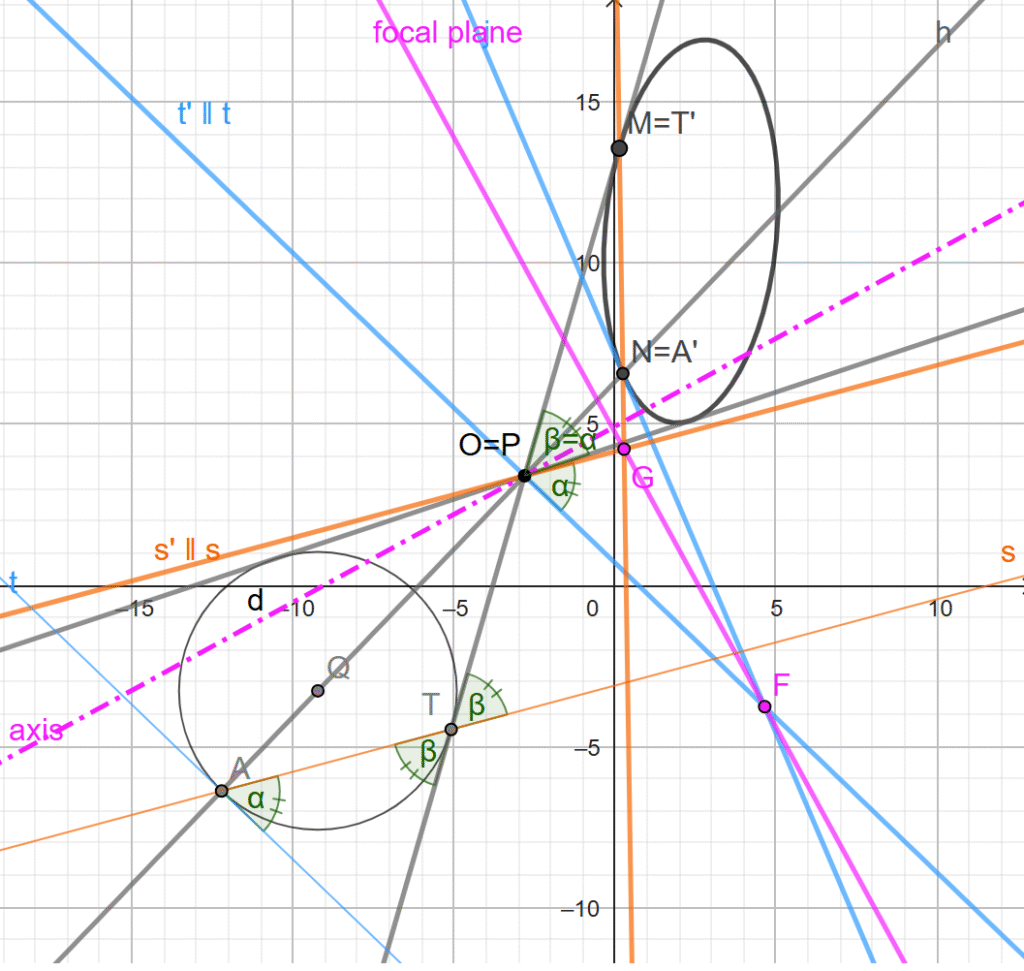
All rays that pass through the optical center O are undeviated by the lens. Therefore, the tangent lines to the ellipse drawn from O are also tangent to the object circle. The bisector h of the angle formed by these tangents must pass through the center of the circle, Q.
Let A be the point on the circle farthest from O. A ray t, tangent to the circle at A (and hence perpendicular to h), continues after passing through the lens as a line tangent to the ellipse at A’ (the blue lines in the figure). This refracted ray will meet a parallel, undeviated line t’ through O, constructed as the perpendicular to h, at a point F that is located on the focal plane.
Let T be the point where one of the tangent lines from O meets the circle. The angles \alpha and \beta shown in the figure are equal, due to symmetry or because they are both inscribed angles of the arc AT. Hence, the line s’, which is parallel to AT through O, is the bisector of the angle formed by lines t’ and OM and can be constructed as such. This undeviated orange ray s’ then meets the refracted ray from AT (the orange line A’T’) at a point G that is also on the focal plane.
Thus, the focal plane is found as the purple line FG, and the optical axis is its perpendicular through O.
You can download the .ggb files of this solution with only construction steps, and together with the explaining elements.