2022-P4 Best Solutions and Final Results

Problem 4 – Image of a point

By the end of the competition, there were 1146 registered participants from 80 countries. In total, 50 solutions were submitted for problem 4, out of which 43 were correct.

As usual, when selecting the best solutions, preference has been given to those solutions which have been submitted before the publication of the first hint. Overall, there were 35 such solutions. Out of those, the pre-screening passed those whose construction in GeoGebra had 25 or less construction steps (marking a point, drawing a circle or a line); there were 23 such submissions. Out of those, the best solution awards got the solutions which were clearly written and did not have gaps in reasoning (e.g. it was not clearly explained why there is a certain freedom to choose the position of the lens). As a result, the best solutions can be divided into three categories.
Solutions – based on harmonic conjugates of projective geometry – with these constructions, compass is not needed, the point D’ can be found by using a ruler and pencil only:
Vlad-Stefan Oros, 19 steps without using a compass (20% of the bonus); ggb file.
Solutions based on cross ratio of projective geometry :
Zhening Li & Eddie Chen, 17 steps (20% of the bonus); ggb file.
Kevin You, 12 steps (20% of the bonus); ggb file.
Erik Sünderhauf, 20 steps without using a compass (20% of the bonus); ggb file.
As a matter of fact, the construction of Erik is very close to the one which is obtained when harmonic bundles are used. Apart from those four, I gave a bonus also to two slightly less rigorous solutions which did not mention projective geometry theorems, but still ended up with constructions close to the ones based on the cross ratio:
Alessandro Rezzi, 13 steps (10% of the bonus): ggb file.
Isaac Wu, 15 steps (10% of the bonus); ggb file.

Finally, a few comments on the solution and my own (JK) ggb file (cf below).
First, many contestants showed nicely and mathematically that an image of a straight line is another straight line, and those two lines meet at the lens. However, the mathematical proof is superfluous once you apply the construction rules of geometrical optics: let a light ray propagate along the original straight line, and refract on the lens. According to the construction rules, the ray propagates after refraction as a straight line, and that is exactly the image of your original line! Since the refraction takes place at the lens, the image and the original obviously meet on the lens.
Second, while knowing the projective geometry was definitely helpful, the problem could have been solved nicely and more or less rigorously without that. As a first step, notice that what the three points (A’, B’, C’) define is only the intersection point F of the line A’B’ with the nearest focal plane, and nothing else, because we don’t know anything about the distance between the original points, and the direction of the line AB. The fact that F (and D’) is uniquely defined can be seen easily by using the Newtonian lens formula. To that end, notice that the distances of the points A’, B’, C’, and D’ from F are proportional to their distances from the respective focal plane (these distances appear in the Newtonian lens formula).

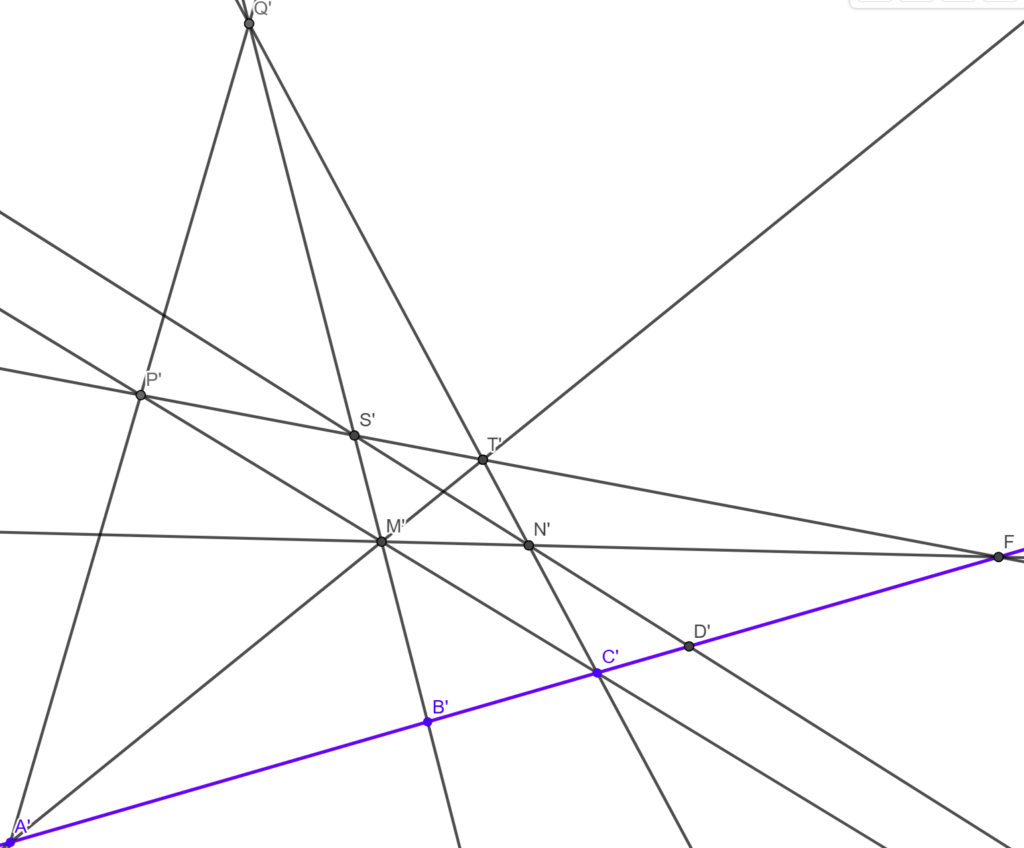
Since only one point of the focal plane is defined, and all those lens positions which yield the same position for that point are legitimate and result in the same position for D’, we are free to add another constraint, e.g. mark arbitrary points P’ and Q’, and demand that these are images of such points P and Q that their originals P and Q form together with the point A another set of equidistant points on a straight line. In other words, we have an image of a triangle AQC, so that the points P and B, the originals of P’ and B’, are the midpoints of AQ and AC, respectively. Hence we can draw the images of the medians, P’C’ and Q’B’, together with their intersection point M’. So, A’M’ is a median, too, and its intersection point T’ with Q’C’ is the image of the midpoint T of QC. Hence, PT is parallel to AC so that their images, the lines P’T’ and A’C’, must meet at the focal plane, at the point F. Now we can draw the image of a line parallel to AC and passing through M; this is the line M’F, and mark its intersection point N’ with the line Q’C’. Finally, we draw line S’N’ and mark its intersection point with line A’C’ as D’. In order to show that |CD| equals to |AB|, we can use the similarity of the triangles ABC and MST, as well as STN amd NCD.

Final results for Problem 5

University students

First name	Surname	Country	School/University	P4 Score
Erik	Sünderhauf	Germany	Technical University of Munich	3.168
Alessandro	Rezzi	Italy	University of Padova	2.6059
Ziyue	Wang	China	Hebei University of Technology	2.1436
Kevin	You	United States	Carnegie Mellon University	1.9671
Yuechen	Zhu	China	Peking University	1.9487
Jaroslav	Herman	Czech Republic	Charles University	1.7716
Zhening Li	Eddie Chen	Canada/United States	Massachusetts Institute of Technology	1.4779
Shofar	Sno	Suriname	Anton de Kom University of Suriname	1.4641
Qian	Lin	China	University of Oxford	1.331
Isaac	Wu	Australia	University of Melbourne	1.1052
Ameya Vikrama	Singh	India	Indian Institute of Technology Bombay	1.1
Marinus	Lehmann	Germany	University of Potsdam	1.0
Bayram Alp	Sahin	Turkey	Bogazici University	1.0
Felix	Schwarzfischer	Germany	Technical University Munich	1.0
Soumyadeep	Sarma	India	Indian Institute of Science	0.9
Cheng Wei	Lin	Taiwan	National Cheng Kung University	0.7
Pushp	Raj	India	IIT DELHI	0.7
Udhav	Varma	India	Indian Institute of Technology, Kanpur	0.7
Simon	Selg	Estonia	Tartu Ülikool	0.5

Pre-university students

First name	Surname	Country	School/University	P4 Score
Vlad-Ștefan	Oros	Romania	“Grigore Moisil” Theoretical High School	3.168
Luca	Milanese	Italy	Liceo “Leonardo da Vinci”, Terracina	2.3579
Adam	Džavoronok	Slovakia	Gymnázium Poštová 9	2.1436
Chengkai	Yu	China	The High School Affiliated to Renmin University of China	1.9487
Wang	Quanquan	China	Tianjin Yaohua High School	1.7716
Yehyun	Choi	United States	Westlake High School	1.6105
Emerson Franzua	Aldana Gavarrete	Honduras	School	1.4641
Sebastián	Arévalo	El Salvador	Instituto Emiliani	1.331
Filip	Vučić	Croatia	I. gymnasium Zagreb	1.21
Tomas	Babelis	Lithuania	Vilniaus jėzuitų gimnazija	1.0
Sarthak	Panda	India	FIITJEE Bhubaneswar	1.0
Vuk	Hip	Serbia	Mathematical Grammar School	1.0
Matej	Gelev	North Macedonia	Yahja Kemal	1.0
Dženan	Midžić	Bosnia and Herzegovina	JU Gimnazija “Bihać”	1.0
Felix	Yew	Malaysia	National Junior College, Singapore	1.0
Azimuddin	Sheikh	India	FIITJEE	1.0
Jun Lin	Jinhua Zhang	China	Lvliang Fengshan Senior Middle School	1.0
Yijun	Lin	China	High School Attached to Herbin Normal University	0.99
Gigi	Tsirekidze	Georgia	LEPL Kutaisi Andria Razmadze physics and mathematical public school N41	0.9
Juan Francisco	Lorusso Notaro Francesco	United Kingdom	Abbey College Cambridge	0.9
Yang Yi	Tang Guofeng	China	Chongqing Nankai Secondary School	0.9
Rhythm	Kedia	India	Lord Buddha Public school	0.72
Miguel Isaías	Doradea Meléndez	El Salvador	Insituto Emiliani	0.5
Mayank	Anand	India	FIITJEE	0.3679

Participating countries: Algeria, Azerbaijan, Australia, Bangladesh, Belarus, Belgium, Bosnia and Herzegovina, Bolivia, Brazil, Bulgaria, Cambodia, Canada, China, Croatia, Czechia, Egypt, El Salvador, Estonia, Finland, Georgia, Germany, Greece, Hungary, India, Indonesia, Iran, Israel, Italy, Japan, Kazakhstan, Kenya, Korea, Kyrgyzstan, Latvia, Lebanon, Lithuania, Macedonia, Malaysia, Mexico, Moldova, Mongolia, Nepal, Nigeria, North Macedonia, Pakistan, Peru, Philippines, Poland, Romania, Russia, Saudi Arabia, Serbia, Singapore, Slovakia, Slovenia, South Africa, South Korea, Spain, Sri Lanka, Sweden, Switzerland, Syria, Taiwan, Thailand, Turkey, Turkmenistan, United Arab Emirates, United Kingdom, United States, Uzbekistan, Vietnam.